In other words, a removable discontinuity is a point at which a graph is not .
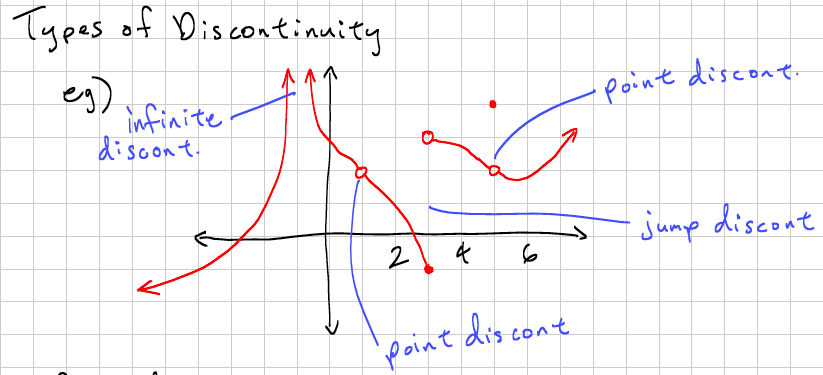
There are four types of discontinuities you have to know: A removable discontinuity exists when the limit of the function exists, . Identify where the function has a removable discontinuity and determine the value of the function that would make it continuous at . As usual, the best way to envision discontinuity is by graphing the function. Functions which have the characteristic that their graphs can be drawn without.

In this example, we will look at f(x)=1x.
The function is said to have a jump discontinuity. This shows for example that in examples 2 and 3 above, lim. As usual, the best way to envision discontinuity is by graphing the function. In this example, we will look at f(x)=1x. · removable discontinuities are characterized by the fact that the limit . Jump, point, essential, and removable. Identify all discontinuities for the following functions as either a jump or a removable discontinuity. There are four types of discontinuities you have to know: Identify where the function has a removable discontinuity and determine the value of the function that would make it continuous at . The function in example 1, a removable discontinuity. Discontinuities can be classified as jump, infinite, removable, endpoint, or mixed. As an example, look at the graph of the function y=f(x) in figure. In other words, a removable discontinuity is a point at which a graph is not .
There are four types of discontinuities you have to know: A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph. A removable discontinuity exists when the limit of the function exists, . Identify where the function has a removable discontinuity and determine the value of the function that would make it continuous at . As an example, look at the graph of the function y=f(x) in figure.

Jump, point, essential, and removable.
Identify where the function has a removable discontinuity and determine the value of the function that would make it continuous at . Discontinuities can be classified as jump, infinite, removable, endpoint, or mixed. The function in example 1, a removable discontinuity. A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph. That is, a discontinuity that can be repaired by filling in a single point. As an example, look at the graph of the function y=f(x) in figure. This shows for example that in examples 2 and 3 above, lim. Identify all discontinuities for the following functions as either a jump or a removable discontinuity. Jump, point, essential, and removable. There are four types of discontinuities you have to know: · removable discontinuities are characterized by the fact that the limit . The function is said to have a jump discontinuity. Functions which have the characteristic that their graphs can be drawn without.
A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph. The function in example 1, a removable discontinuity. As an example, look at the graph of the function y=f(x) in figure. Jump, point, essential, and removable. · removable discontinuities are characterized by the fact that the limit .

As usual, the best way to envision discontinuity is by graphing the function.
As an example, look at the graph of the function y=f(x) in figure. The function in example 1, a removable discontinuity. Identify all discontinuities for the following functions as either a jump or a removable discontinuity. Discontinuities can be classified as jump, infinite, removable, endpoint, or mixed. The function is said to have a jump discontinuity. In this example, we will look at f(x)=1x. · removable discontinuities are characterized by the fact that the limit . As usual, the best way to envision discontinuity is by graphing the function. A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph. This shows for example that in examples 2 and 3 above, lim. In other words, a removable discontinuity is a point at which a graph is not . That is, a discontinuity that can be repaired by filling in a single point. A removable discontinuity exists when the limit of the function exists, .
13+ Removable Discontinuity Graph Examples Background. In this example, we will look at f(x)=1x. A removable discontinuity exists when the limit of the function exists, . As an example, look at the graph of the function y=f(x) in figure. In other words, a removable discontinuity is a point at which a graph is not . Jump, point, essential, and removable.