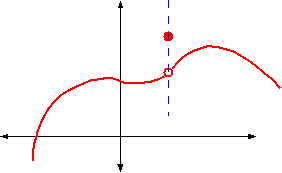
Geometrically, a removable discontinuity is a hole in the graph of f.
If it really is a removable discontinuity, then filling in the hole results in a continuous graph! Find a point of discontinuity : Such a point is called a removable discontinuity. Both the limits are finite and equal: Please see the explanation section, below.

Both the limits are finite and equal:
A function, f , is continuous at a number, a if and only if . Please see the explanation section, below. Let's take a look at the graph below. Example 1 of discontinuous function fig 2. For example, consider the following function: Both the limits are finite and equal: Such a point is called a removable discontinuity. A removable discontinuity occurs when the graph of a function has a hole. Find a point of discontinuity : The function in example 1, a removable discontinuity. Geometrically, a removable discontinuity is a hole in the graph of f. Temperature as a function of time is an example of a continuous function. If it really is a removable discontinuity, then filling in the hole results in a continuous graph!
For example, consider the following function: Such a point is called a removable discontinuity. Both the limits are finite and equal: Temperature as a function of time is an example of a continuous function. Find a point of discontinuity :

For example, consider the following function:
Example 1 of discontinuous function fig 2. As shown in the graph has jump of . If it really is a removable discontinuity, then filling in the hole results in a continuous graph! Find a point of discontinuity : Please see the explanation section, below. A removable discontinuity occurs when the graph of a function has a hole. Geometrically, a removable discontinuity is a hole in the graph of f. Graph of function f with a removable discontinuity at x=a. Such a point is called a removable discontinuity. Temperature as a function of time is an example of a continuous function. A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph. The function in example 1, a removable discontinuity. Both the limits are finite and equal:
Temperature as a function of time is an example of a continuous function. Set the removable discontinutity to zero and solve for the location of the hole. Find a point of discontinuity : Geometrically, a removable discontinuity is a hole in the graph of f. Graph of function f with a removable discontinuity at x=a.

Let's take a look at the graph below.
The function in example 1, a removable discontinuity. Temperature as a function of time is an example of a continuous function. Geometrically, a removable discontinuity is a hole in the graph of f. Both the limits are finite and equal: A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph. Graph of function f with a removable discontinuity at x=a. A removable discontinuity occurs when the graph of a function has a hole. Please see the explanation section, below. Such a point is called a removable discontinuity. As shown in the graph has jump of . A function, f , is continuous at a number, a if and only if . Let's take a look at the graph below. Example 1 of discontinuous function fig 2.
36+ Removable Discontinuity Example Images. Please see the explanation section, below. If it really is a removable discontinuity, then filling in the hole results in a continuous graph! Find a point of discontinuity : Set the removable discontinutity to zero and solve for the location of the hole. A removable discontinuity occurs when the graph of a function has a hole.