Therefore, x = 3 and x =7 are both infinite discontinuities of h, as well as the locations of vertical asymptotes on the graph of h.
Occasionally, a graph will contain a hole: 1 this use is improper because continuity and discontinuity of a function are concepts defined only for points in the function's domain. An essential discontinuity can't be Imagine you're walking down the road, and someone has removed a manhole cover (careful! Types of discontinuities (i) removable (ii) jump (iii) infinite nonremovable at a particular point we can classify three types of discontinuities.

(or swath of holes) in the graph of the function that could be filled (or a singleton point that can be moved/redefined) so as to make the function continuous there.
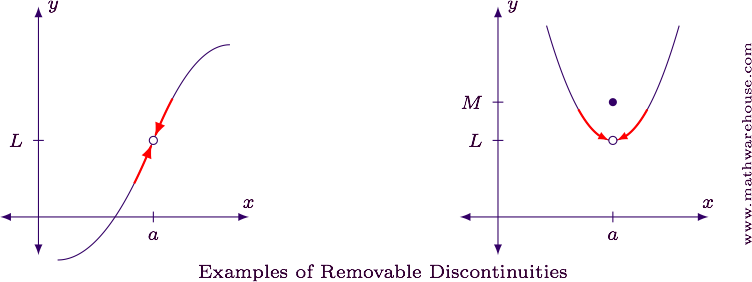
If a function is not continuous at a point in its domain, one says that it has a discontinuity there. A removable discontinuity has a gap that can easily be filled in, because the limit is the same on both sides. For instance, the function f(x) = (x — 1)^2 / (x — 1) has a limit equal to 0 as x goes to 1, but is not defined at x. Therefore, x = 3 and x =7 are both infinite discontinuities of h, as well as the locations of vertical asymptotes on the graph of h. Types of discontinuities (i) removable (ii) jump (iii) infinite nonremovable at a particular point we can classify three types of discontinuities. By filling in a single point. point discontinuities exist for piecewise functions where a specific value for x is defined differently than the rest of the piecewise function. Similarly, calculus in maths, a function f(x) is continuous at x = c, if there is no break in the graph of the given function at the point. Some discontinuities are classified as removable discontinuities. We cannot redefine the function. Let's call this mathf(x) = \frac{\sin x}{x}/math. The zeros at x = 3 (after a partial cancellation of one of two copies) and at x =7 remain. But their common value is not equal to f(a).
This type of discontinuity is known as discontinuity of first kind. In this case, we can redefine the function such that limit ₓ→ c f(x) = f (c) and make it continuous at x=c. Graph of the discontinuous function listed below x +1 x > The function is continuous everywhere except one point for example, g (x) = sin(x) and h 1−cos x x are defined for x = 0, but x both functions have removable discontinuities. Until this point, our main focus was limits and how to determine them.

Tap again to see term 👆.
For example, let's look at the following piecewise function: Let's call this mathf(x) = \frac{\sin x}{x}/math. I can calculate the needed function value to retain a limit and create continuity. In this case, we can redefine the function such that limit ₓ→ c f(x) = f (c) and make it continuous at x=c. When a rational function has a vertical asymptote as a result of the denominator being equal to zero at some point, it will have an infinite discontinuity at that point. That is, a discontinuity that can be "repaired" If a function is not continuous at a point in its domain, one says that it has a discontinuity there. In either of these two cases the limit can be quantified and the gap can be removed; T his is the first topic dealing with continuity in unit 1. However, a large part in finding and determining limits is knowing whether or not the function is continuous at a certain point. I tried making sense of it by just drawing the two functions of f (x), but i'm not sure how to find the points of discontinuity for these. removable discontinuity graph download scientific diagram. A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph.
However, a large part in finding and determining limits is knowing whether or not the function is continuous at a certain point. Continuous functions are of utmost importance in mathematics and applications. The functions that are not continuous can present different types of discontinuities. Tap card to see definition 👆. For example, let's look at the following piecewise function:

In either of these two cases the limit can be quantified and the gap can be removed;
If a function is not continuous at a point in its domain, one says that it has a discontinuity there. H (x) = note that for removable discontinuity, lim x → x 0 f (x) must exist. Occasionally, a graph will contain a hole: A function f defined on an interval i ⊆ r is said to have removable discontinuity at x 0 ∈ i if there is a function h:i→r such that. However, not all functions are continuous. First, however, we will define a discontinuous function as any function that does not satisfy the definition of continuity. Imagine you're walking down the road, and someone has removed a manhole cover (careful! That is, a discontinuity that can be "repaired" A function is continuous on an interval if we can draw the graph from start to finish without ever once picking up our pencil. A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph. Lim xa f (x) does not exist. Continuous functions are of utmost importance in mathematics and applications. There are several types of behaviors that lead to discontinuities.
Get Point Removable Discontinuity Definition Background. (or swath of holes) in the graph of the function that could be filled (or a singleton point that can be moved/redefined) so as to make the function continuous there. Lhl and rhl are finite but not equal. For instance, the function f(x) = (x — 1)^2 / (x — 1) has a limit equal to 0 as x goes to 1, but is not defined at x. From the definition of removable discontinuity, it occurs at points where the. removable discontinuities are those where there is a hole in the graph as there is in this case.