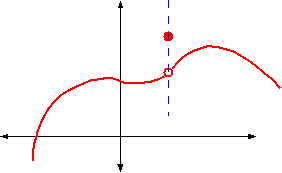
Let's look at the function \(y=f(x)\) represented by the graph in figure.
By filling in a single point. In other words, a function will yield a result of when f(x) = the removable discontinuity. For example, consider a polynomial function p ( x). If the graph has a closed dot. There are no vertical asymptotes.

And removable discontinuity at x equal to four.
From this example we can get a quick "working" (often jump or infinite discontinuities.) definition. When graphed, a removable discontinuity is marked by an open circle on the graph at the point where the graph is undefined or is a different value like this. The function is not continuous because there is a hole.in this case, all limits exist. A function is continuous on an interval if we can draw the graph from start to finish without ever once picking up our pencil. A removable discontinuity is defined as follows: We factor the numerator and denominator and check for common factors. A point on the graph that is undefined or is unfit for the rest of the graph is known as a removable discontinuity. An essential discontinuity (also called second type or irremovable discontinuity) is a discontinuity that jumps wildly as it gets closer to the limit. A removable discontinuity is a point on the graph that is missing or separate from the rest of the function. An example of the corresponding function graph is shown in the figure below: In this lesson you will examine three other types of discontinuities: It could be like this.
We know the domain of p ( x) is the set of all reals. There are several types of behaviors that lead to discontinuities. Wataru · · sep 20 2014 So this jump discontinuity at x equal to two. There are many examples of continuous functions.

The graph of a removable discontinuity leaves you feeling empty, whereas a graph of a nonremovable discontinuity leaves you feeling jumpy.
A removable discontinuity exists when the limit of the function exists, but one or both of the other two conditions is not met. A removable discontinuity occurs in the graph of a rational function at x = a x = a if a a is a zero for a factor in the denominator that is common with a factor in the numerator. Identify a rational function whose graph is a horizontal line except for two holes. Set the removable discontinutity to zero and solve for the location of the hole. A function \(f\) is continuous at \(x=a\) when we can determine its limit at \(x=a\) by substitution. So it can be like this. removable discontinuities are so named because one can "remove" Classify each discontinuity as either jump, removable, or infinite. Okay, i presume that the brackets denote the greatest. The point, or removable, discontinuity is only for a single value of x, and it looks like single points that are separated from the rest of a function on a graph. So this is the removable discontinuity. To find the point of a discontinuity, factor the function's denominator. How to graph the above function:
Consider the function f (x) = 1/x. This in combination with one of our limit laws, " This type of function is said to have a removable discontinuity. removable discontinuity graph post by localghost » sat apr 10, 2010 3:23 pm gmedina wrote: If a function f is continuous, has no cusps or vertical asymptotes, and it's only defect is that it has a removable discontinuity at x = c, let's just say plainly that it has a hole at x = c, then according to this form of the derivative of f.
Identify any points of discontinuity, and determine (giving reasons) if they are removable, infinite (essential), or jump discontinuities.
Below is the graph for f (x) = (x + 2) (x + 1) x + 1. In other words, a removable discontinuity is a point at which a graph is not connected but can be made connected by filling in a single point. There are several types of behaviors that lead to discontinuities. There are many examples of continuous functions. Geometrically, a removable discontinuity is a hole in the graph of #f#. When discont is true or a list, then the procedure described above for detecting discontinuities is followed. Classify each discontinuity as either jump, removable, or infinite. If #f# has a discontinuity at #a#, but #lim_(xrarra)f(x)# exists, then #f# has a removable discontinuity at #a# ("infinite limits" \(\lim_{x\rightarrow a}f(x)\neq f(a)\) this type of discontinuity can be easily eliminated by redefining the function. The function has a limit. The discont option takes values true and false, with false being the default. A function \(f\) is continuous at \(x=a\) when we can determine its limit at \(x=a\) by substitution. In this lesson you will examine three other types of discontinuities:
Download Removable Discontinuity Graph PNG. This makes it difficult to remove the gap (hence the alternate name, "irremovable" Identify a rational function whose graph is a horizontal line except for two holes. Tells us that lim x → c p ( x) and p ( x) both exist and agree in. Consider the graph of the function y = f (x) y = f (x) shown in the following graph. Get an answer for 'is a graph still continuous and differentiable if it has a removable discontinuity?