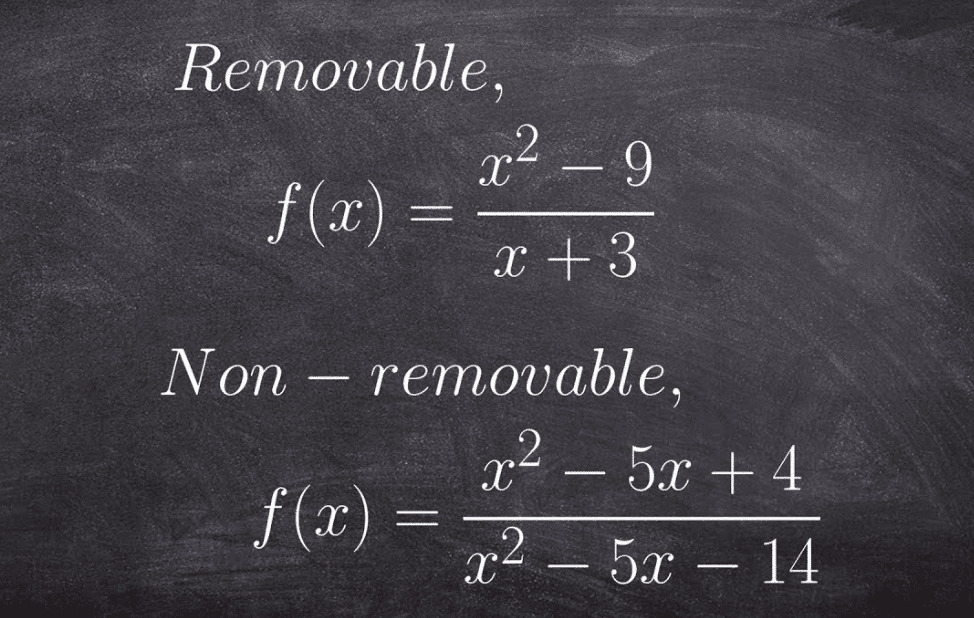Sketch the graph of a function that has a jump discontinuity at x = 2 and a removable discontinuity at x = 4, but is continuous elsewhere.:
The graph of f has a horizontal asymptote at y 3, and f has a removable discontinuity at x 2 (a) show that a 6 and b 13 (b) to make f continuous at x 2 f 2 should be defined as what value? I really have no clue what this question is asking me. Sketch the graph of a function that has a jump discontinuity at x = 2 and a removable discontinuity at x = 4, but is continuous elsewhere.: = sin ( π/4) = 1/√2. For the values of x lesser than or equal to π/4, we have to choose the function sin x.

(you may get none, but there can be more than one.) note that if there are no removable discontinuities or vertical asymptotes, the function is continuous.
There is no discontinuity at x = 3. Is the discontinuity of f (x) = sin (pi x)/3x at x=0 removable? 4210 9 3 xx fx x −+ = − 7. Sketch the graph of a function that has a jump discontinuity at x = 2 and a removable discontinuity at x = 4, but is continuous elsewhere.: Let us examine where f has a discontinuity. 3244 1 xx x fx x +−− = + 8. The equation is undefined where the denominator equals 0 0, the argument of a square root is less than 0 0, or the argument of a logarithm is. removable discontinuities are shown in a graph by a hollow circle that is also known as a hole. 131) f(x) = 1 √x. Here we have a graph which has the desired discontinuities. The point, or removable, discontinuity is only for a single value of x, and it looks like single points that are separated from the rest of a function on a graph. If we find any, we set the common factor equal to 0 and solve. removable discontinuities of rational functions.
If it really is a removable discontinuity, then filling in the hole results in a continuous graph! 3244 1 xx x fx x +−− = + 8. The vertical graph occurs where the rational function for value x, for which the denominator should be 0. I can identify which part of the definition is violated for each kind of discontinuity. There are four types of discontinuities you have to know:

Essentially, a removable discontinuity is a point on a graph that doesn't fit the rest of the graph or is undefined.
Consider the function 𝑓 ( 𝑥 ) = ⎧ ⎨ ⎩ 6 𝑥 − 8 𝑥 + 2 3 𝑥 − 1 𝑥 ≠ 1 3 , − 4 3 𝑥 = 1 3. Vertical asymptote are known as vertical lines they corresponds to the zero of the denominator were it has an rational functions. Use a calculator to find an interval of length 0.01 that contains a solution. Evaluate for each of the following functions: An essential discontinuity (also called second type or irremovable discontinuity) is a discontinuity that jumps wildly as it gets closer to the limit. discontinuity) and perform any calculations on the function. The function is defined for all x in the interval ( 0, ∞). H x x ln (a) h 0 (b) 0 lim x hx o (c) 0 lim x hx o (d) 0 lim x hx o s ii. Function off their calculators and take a closer look at the rational function. The function f (x) has a discontinuity of the first kind at x = a if. No calculator is allowed for this question 2. If we find any, we set the common factor equal to 0 and solve. Discontinuities as values of x where "holes"
An essential discontinuity (also called second type or irremovable discontinuity) is a discontinuity that jumps wildly as it gets closer to the limit. A removable discontinuity is a point on the graph that is undefined or does not fit the rest of the graph. Vertical asymptote are known as vertical lines they corresponds to the zero of the denominator were it has an rational functions. Your first 5 questions are on us! Draw an open circle and label any removable discontinuities on the graph.

Here we are going to check the continuity between 0 and π/2.
Let f be the function given by f of x is equal to the square root of x plus 4 minus 3 over x minus 5 if f if x does not equal 5 and it's equal to c if x equals 5 and say if f is continuous at x equals 5 what is the value of c so if we know that f is continuous at x equals 5 that means that the limit the limit as x approaches 5 of f of x is equal to f of 5 this is the definition of continuity. No calculator is allowed for this question 2. The function f (x) has a discontinuity of the first kind at x = a if. D) graph the function using paper and pencil. (you may get none, but there can be more than one.) note that if there are no removable discontinuities or vertical asymptotes, the function is continuous. Draw an open circle and label any removable discontinuities on the graph. I can identify which part of the definition is violated for each kind of discontinuity. When graphing function, you should cancel the removable factor, graph like usual and then insert a hole in the appropriate spot at the end. An essential discontinuity (also called second type or irremovable discontinuity) is a discontinuity that jumps wildly as it gets closer to the limit. The final type of discontinuity is called a "removable" For the values of x lesser than or equal to π/4, we have to choose the function sin x. Compute answers using wolfram's breakthrough technology & Distance between the asymptote and graph becomes zero as the graph gets close to the line.
29+ Removable Discontinuity Calculator Gif. The graph of f has a horizontal asymptote at y 3, and f has a removable discontinuity at x 2 (a) show that a 6 and b 13 (b) to make f continuous at x 2 f 2 should be defined as what value? removable discontinuities are those where there is a hole in the graph as there is in this case. For the values of x greater than π/4, we have to choose the function cos x. Draw an open circle and label any removable discontinuities on the graph. The point, or removable, discontinuity is only for a single value of x, and it looks like single points that are separated from the rest of a function on a graph.